平成23年度春期 エンベデッドシステムスペシャリスト試験 午前II 問6
【問題6】
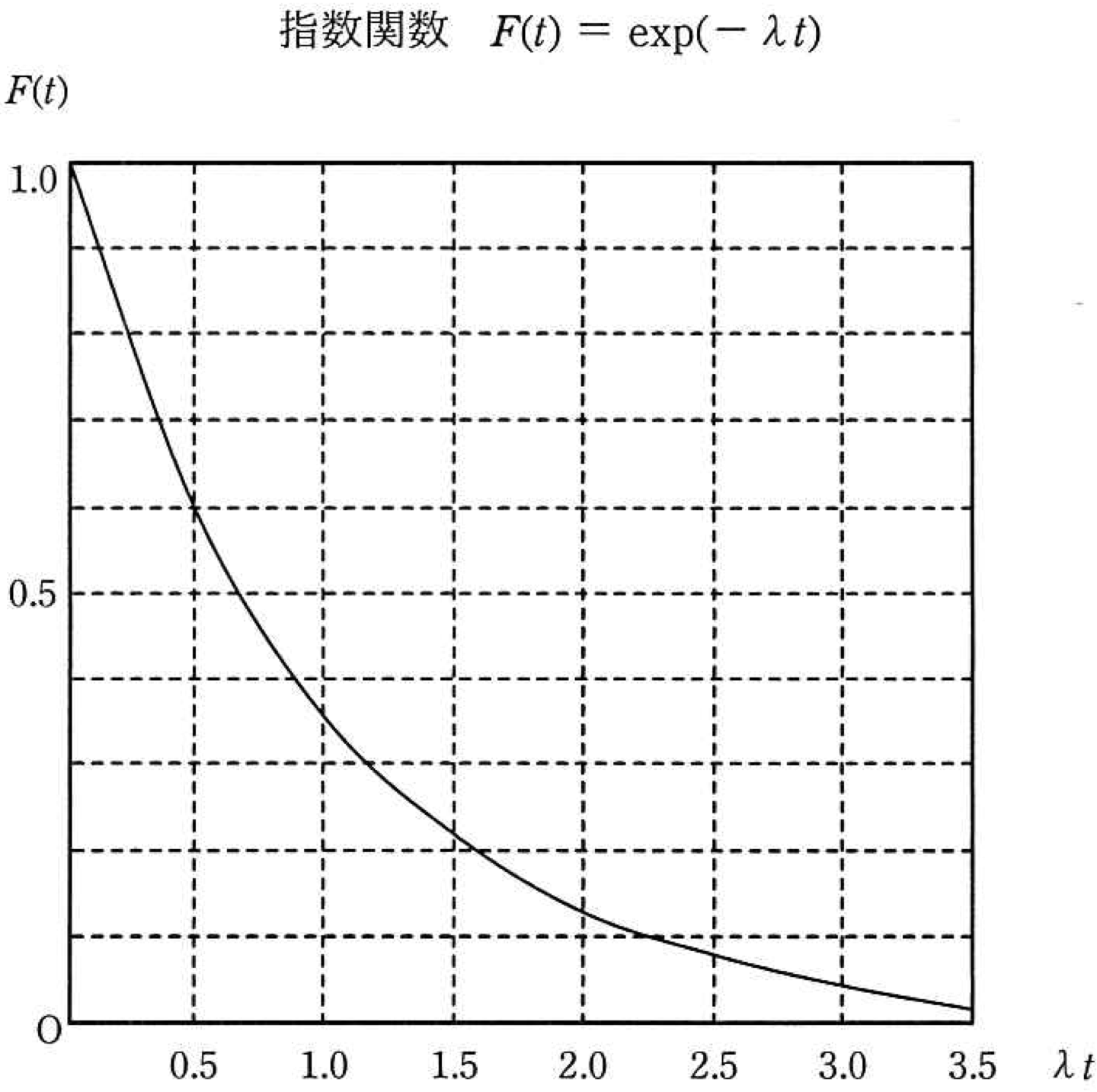
故障発生率が 1.0 × 10⁻⁶ 回/秒である機器 10,000 台が稼働している。330 時間経過後に、故障していない機器の平均台数に最も近いものはどれか。ここで、故障発生率は経過時間にかかわらず一定で、故障した機器は修理しない。また、必要であれば、故障発生率を λ 回/秒、稼働時間を t 秒とする次の指数関数のグラフから値を読み取って、計算に使用してよい。
【解説】
1. 故障発生率(λ)を確認します。
λ = 1.0 × 10⁻⁶ 回/秒
2. 経過時間 t を秒単位に変換します。
t = 330 時間 × 60 分 × 60 秒 = 1,188,000 秒
3. 故障していない割合を指数関数で求めます。
F(t) = exp(-λt) に値を代入します。
F(t) = exp(-1.0 × 10⁻⁶ × 1,188,000)
4. λt を計算します。
λt = 1.0 × 10⁻⁶ × 1,188,000 = 1.188
5. グラフよりexp(-1.188) を求めます。
F(t) ≈ 0.300 (グラフから大体の値を確認)
6. 故障していない機器の台数を計算します。
稼働中の台数 = 10,000 × 0.300 ≈ 3,000 台
7. 最も近い選択肢は **ア: 3,000** です。
出典:平成23年度 春期 エンベデッドシステムスペシャリスト試験 午前II 問6
